The Main Reason You Need to Know the Projection of Data
![]()
Projections and Coordinate Systems
Projections and coordinate systems are a complicated topic in GIS, just they course the basis for how a GIS can store, analyze, and display spatial data. Understanding projections and coordinate systems important knowledge to have, particularly if yous deal with many different sets of data that come from different sources.
Projections
Baloney
Coordinate Systems
Datums
Examples of different projections
Projection Storage vs. Definition
Projecting spatial datasets
How projections work on a programmatic level
Projections
The best model of the earth would be a three-dimensional solid in the same shape as the world. Spherical globes are oft used for this purpose. Nonetheless, globes take several drawbacks.
- Globes are large and cumbersome.
- They are generally of a scale unsuitable to the purposes for which most maps are used. Usually we desire to come across more item than is possible to be shown on a earth.
- Standard measurement equipment (rulers, protractors, planimeters, dot grids, etc.) cannot be used to mensurate distance, angle, expanse, or shape on a sphere, every bit these tools have been constructed for use in planar models.
- The latitude-longitude spherical coordinate organisation can just be used to measure angles, non distances or areas.
Here is an image of a world, displaying lines of reference. These lines can only be used for measurement of angles on a sphere. They cannot be used for making linear or areal measurements.
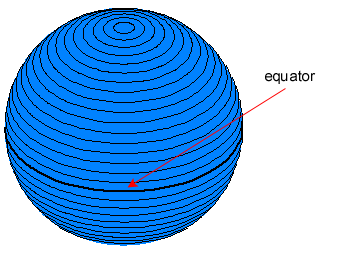 | 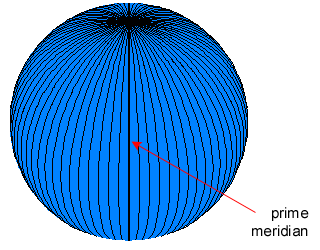 | 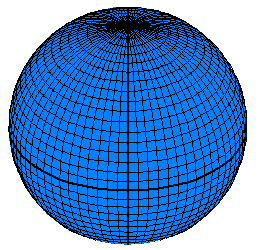 |
| | | |
Positions on a earth are measured by angles rather than X, Y (Cartesian planar) coordinates. In the image beneath, the specific point on the surface of the world is specified by the coordinate (threescore °. E longitude, 55 den. N latitude). The longitude is measured as the number of degrees from the prime meridian, and the breadth is measured as the number of degrees from the equator.
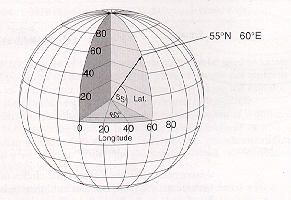
[Paradigm from ESRI]
For this reason, projection systems have been adult. Map projections are sets of mathematical models which transform spherical coordinates (such as latitude and longitude) to planar coordinates (ten and y). In the process, data which really prevarication on a sphere are projected onto a flat plane or a surface. That surface tin exist converted to a planar department without stretching.
Here is a simple schematic designed to show how a project works. Imagine a glass sphere marked with grid lines or geographic features. A lite positioned in the center of the sphere shines ("projects") outward, casting shadows from the lines. A aeroplane, cone, or cylinder (known as a developable surface) is placed outside the sphere. Shadows are bandage upon the surface. The surface is opened flat, and the geographic features are displayed on a flat plane. As soon as a projection is practical, a Cartesian coordinate system (regular measurement in X and Y dimensions) is implied. The user gets to choose the details of the coordinate system (e.g., units, origin, and offsets).
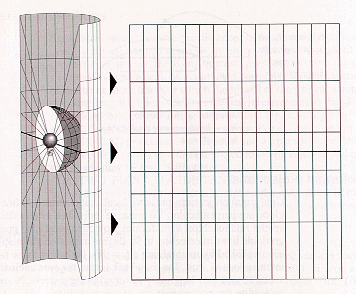
[Paradigm from ESRI ]
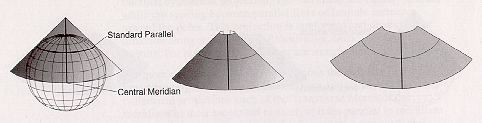
The projection surfaces (i.e., cylinders, cones, and planes) form the basic types of projections:
| Conic |  | The conic tangent case: The conic secant example: Standard parallels are where the cone touches or slices through the globe. Conic projections are used frequently for mapping large areas (e.g., states, large countries, or continents). |
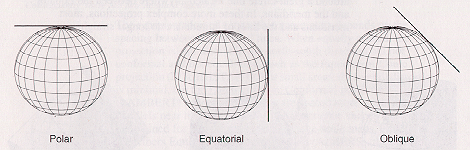
| Cylindrical |  | Dissimilar cylindrical projection orientations: The most mutual cylindrical projection is the Mercator projection, which is the ground of the UTM (Universal Transverse Mercator) arrangement. |
| Planar (Orthographic) |  | Different orthographic project parameters: |
Distortion
Notice in these images how distortion in distance is minimized at the place on the surface that is closest to the sphere. Distortion increases every bit you travel forth the surface farther from the light source. This distortion is an unavoidable belongings of map projection. Although many unlike map projections be, they all introduce baloney in one or more of the following measurement backdrop:
- Shape
- Altitude
- Truthful Direction
- Area
Distortion will vary in at least one of each of the above properties depending on the projection used, also as the scale of the map, or the spatial extent that is mapped. Whenever 1 type of distortion is minimized, at that place will exist respective increases in the distortion of one or more of the other properties.
There are names for the different classes of projections that minimize baloney.
- Those that minimize distortion in shape are called conformal.
- Those that minimize distortion in distance are known every bit equidistant.
- Those that minimize distortion in area are known equally equal-surface area.
- Those minimizing distortion in management are called truthful-direction projections.
It is appropriate to cull a projection based on which measurement properties are most of import to your work. For case, if it is very important to obtain accurate area measurements (e.grand., for determining the home range of an animate being species), you will select an equal-area projection.
Coordinate Systems
One time map data are projected onto a planar surface, features must be referenced by a planar coordinate organisation. The geographic system (latitude-longitude), which is based on angles measured on a sphere, is not valid for measurements on a aeroplane. Therefore, a Cartesian coordinate system is used, where the origin (0, 0) is toward the lower left of the planar section. The true origin point (0, 0) may or may not be in the proximity of the map data you are using.
Coordinates in the GIS are measured from the origin signal. Withal, imitation eastings and false northings are frequently used, which finer offset the origin to a unlike identify on the coordinate plane. This is washed in order to achieve several purposes:
- Minimize the possibility of using negative coordinate values (to make calculations of distance and area easier).
- Lower the absolute value of the coordinates (to make the values easier to read, transcribe, calculate, etc.).
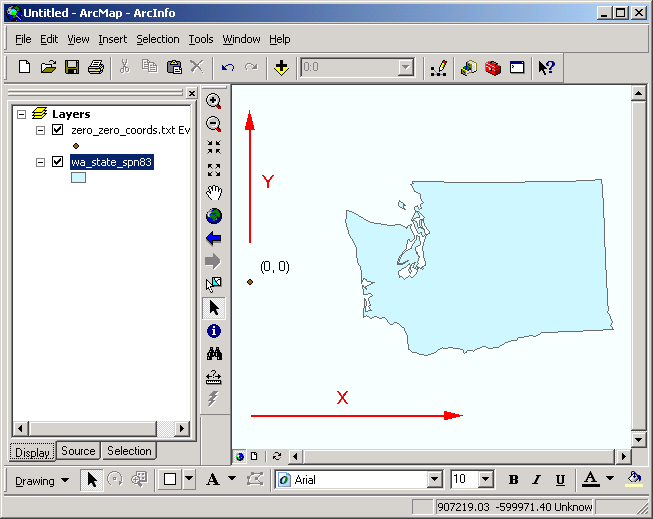
In this prototype, Washington country is projected to State Airplane N (NAD83). All of the locations on the map are now referenced in Cartesian coordinates, where the origin lies several hundred miles off the Pacific declension.
Some measurement framework systems ascertain both projections and coordinate systems. For example, the Universal Transverse Mercator (UTM) system, unremarkably used by scientists and Federal organizations, is based on a serial of 60 transverse Mercator projections, in which different areas of the earth fall into dissimilar 6-degree zones. Within each zone, a local coordinate system is divers, in which the X-origin is located 500,000 m west of the primal meridian, and the Y-origin is the due south pole or the equator, depending on the hemisphere. The State Airplane system as well defines both projection and coordinate system.
The two most common coordinate/projection systems you lot will run into in the U.s. are:
- State Plane
The state plane system includes different projections for each state, and frequently different projections for different areas inside each state. The Country Plane system was adult in the 1930s to simplify and formulate the different coordinate and projection systems for dissimilar states within the USA.
Three conformal projections were called: the Lambert Conformal Conic for states that are longer in the east-west management, such every bit Washington, Tennessee, and Kentucky, the Transverse Mercator projection for states that are longer in the north-south direction, such as Illinois and Vermont, and the Oblique Mercator projection for the panhandle of Alaska, considering it is neither predominantly due north nor due south, but at an oblique angle.
To maintain an accurateness of 1 part in ten,000, information technology was necessary to divide many states into multiple zones. Each zone has its ain central meridian and standard parallels to maintain the desired level of accuracy. The origin is located south of the zone boundary, and false eastings are applied so that all coordinates within the zone will accept positive X and Y values. The boundaries of these zones follow canton boundaries. Smaller states such equally Connecticut require but one zone, whereas Alaska is equanimous of ten zones and uses all three projections.
Washington is divided into 2 zones, a n zone and a south zone. Here are the project parameters for each zone:
| Zone | SPCS Zone # | FIPS Zone # | Project | 1st Std. Parallel | 2nd Std. Parallel | Central Meridian | Origin | Simulated Easting | False Northing |
| WA_N | 5601 | 4601 | Lambert Conformal Conic | 47 thirty 00 | 48 44 00 | -120 50 00 | 47 00 00 | 609601.21920 | 0 |
| WA_S | 5626 | 4602 | Lambert Conformal Conic | 45 50 00 | 47 20 00 | -120 30 00 | 45 20 00 | 609601.21920 | 0 |
- Universal Transverse Mercator (UTM)
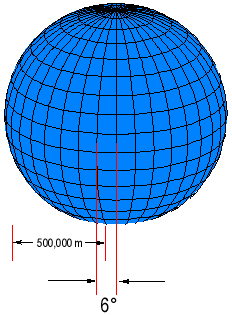
A particular subset of the transverse Mercator is the Universal Transverse Mercator (UTM) which was adopted originally by the US Army for big-scale military maps. In the UTM system, the globe is divided into 60 zones between 84° Due south and 84° N, most of which are 6° wide. Each UTM zone has its own fundamental tiptop and spans 3° due west and 3° east from the center of the zone. Note that the position of the cylinder developable surface is positioned at a unlike place effectually the world for each zone. X- and Y-coordinates are in meters by convention.
For zones in the northern hemisphere, the Ten-origin is a place 500,000 g westward of the fundamental meridian, and the Y-origin is the Equator. The false easting is used to eliminate negative coordinates.
For zones in the southern hemisphere, the Ten origin is besides 500,000 yard west of the central height, but the Y-origin is the South Pole.
UTM Zone layout:
UTM Zone locations and filigree designations:
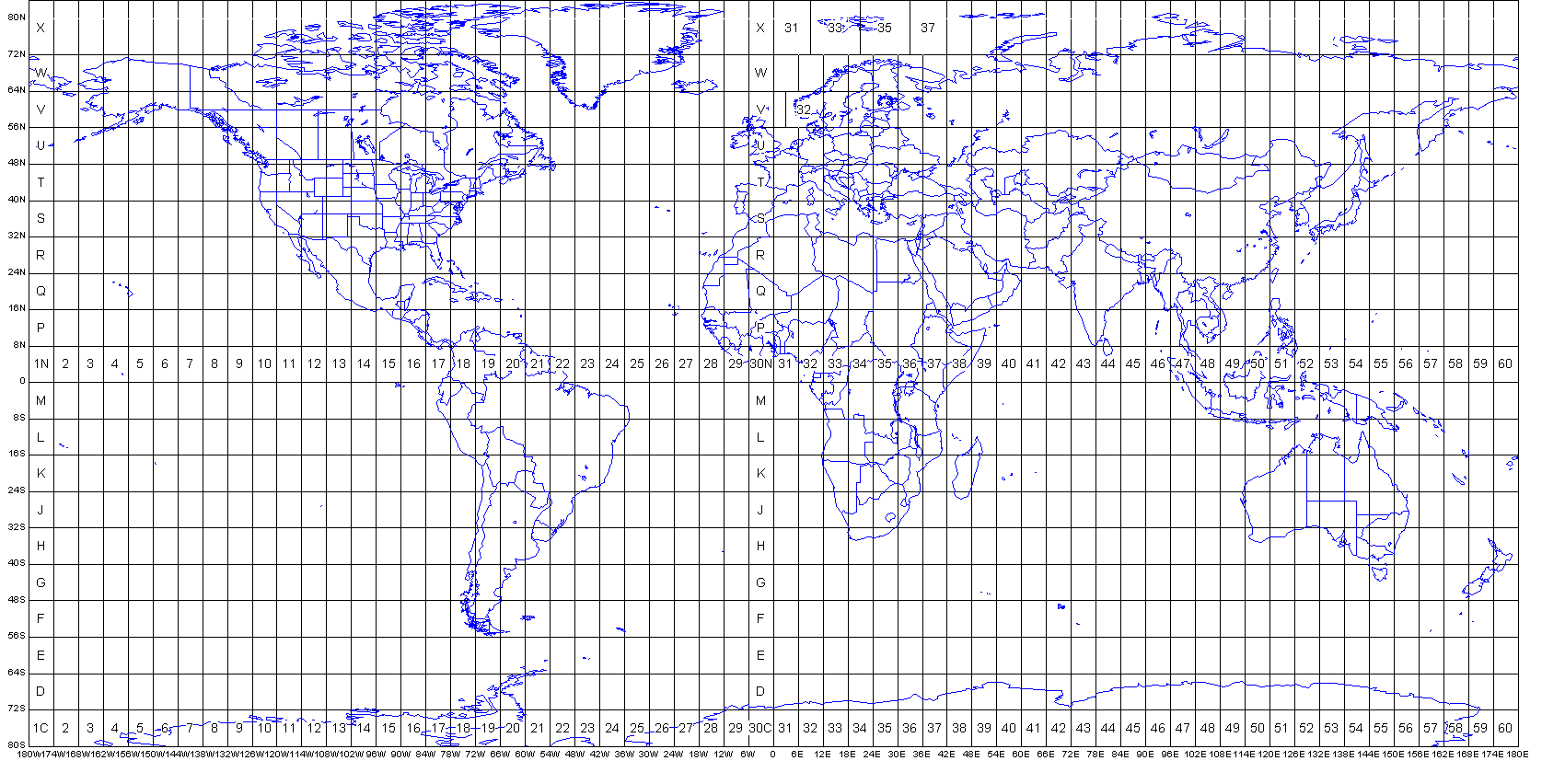
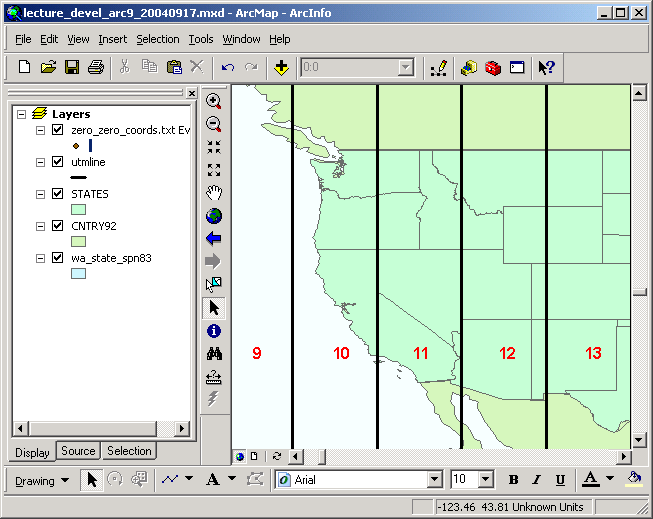
By convention, areas in Washington are mapped in Zone 10 of the UTM system, even though eastern Washington lies in Zone eleven. Zone 10 has its central top at 123° West longitude, and covers the range 126° West -120° W. The Zone's origin is 500,000 one thousand west of 123° W.
Hither are the UTM Zones for the Western United states of america:
Datums
Datums are sets of parameters and footing control points defining local coordinate systems. Considering the earth is non a perfect sphere, but is somewhat "egg-shaped," geodesists utilise spheroids and ellipsoids to model the 3-dimensional shape of the world. Although the earth tin be modeled past an egg-shaped solid, local variations still be, due to differential thickness of the globe's crust, or differential gravitation due to density of the crustal material. A datum is created to account for these local variations in establishing a coordinate system.
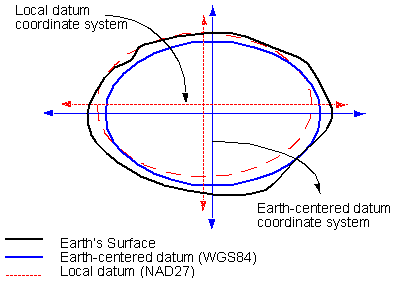
epitome from ESRI
In the image above, the globe is shown every bit the irregular surface (thick blackness line). A generalized globe-centered coordinate system (WGS84, in blue) provides a skilful overall mean solution for all places on the globe. However, for specific local measurements, WGS84 cannot account for local variations. Instead, local datums have been adult. In this case, the local North American Datum of 1927 (NAD27, in dashed red line) more closely fits the earth's surface in the upper-left quadrant of the earth's cross-section. NAD27 merely fits this quadrant, and so to utilize information technology in another part of the globe will consequence in serious errors in measurement. For mapping North America, in order to obtain the well-nigh accurate locations and measurements, NAD27 or NAD83/91 are used.
Project Storage vs. Definition
All spatial datasets are stored with one projection/coordinate organization or another. Even the and then-called "unprojected" datasets, which take their coordinates stored in decimal degrees of breadth and longitude, are using a spatial reference system that is managed by the estimator. This is what is meant by "storage." Every dataset is stored with a spatial reference, regardless of if the spatial referencing system is documented with the dataset.
If a dataset has been built with documentation about its spatial referencing, then information technology is said to accept a project or coordinate organisation "divers." If a dataset has no projection divers, it is possible to apply the software to define the projection, that is, to add extra data that describe the projection and coordinate system of the dataset.
In any case, it is extremely important, as a user, to know the projection and coordinate organization of all the data you utilise. Sometimes datasets will appear to exist incompatible; if this happens, sometimes the only pace necessary to allow the datasets to be used together is to ascertain the projection. Once the project is defined, ArcGIS will exist able to manage the datasets and, if necessary, project one of the datasets on the fly to match the other.
Examples of different projections
Hither is a view of the globe in several different projections, along with cursory descriptions of their properties (descriptions copied from the on-line documentation):
| Mercator (cylindrical) |  Properties Shape: Conformal. Small shapes are well represented because this project maintains the local athwart relationships. Area: Increasingly distorted toward the polar regions. For case, in the Mercator projection, although Greenland is only 1-8th the size of South America, Greenland appears to exist larger. Direction: Any straight line fatigued on this projection represents an actual compass bearing. These true direction lines are rhumb lines, and generally exercise not draw the shortest distance betwixt points. Distance: Scale is true along the Equator, or along the secant latitudes. |
| Miller (cylindrical) |  Properties Shape: Minimally distorted between 45th parallels, increasingly toward the poles. Land masses are stretched more eastward to west than they are n to southward. Area: Distortion increases from the Equator toward the poles. Direction: Local angles are correct only along the Equator. Distance: Correct distance is measured along the Equator. |
| Robinson (pseudo- cylindrical) | 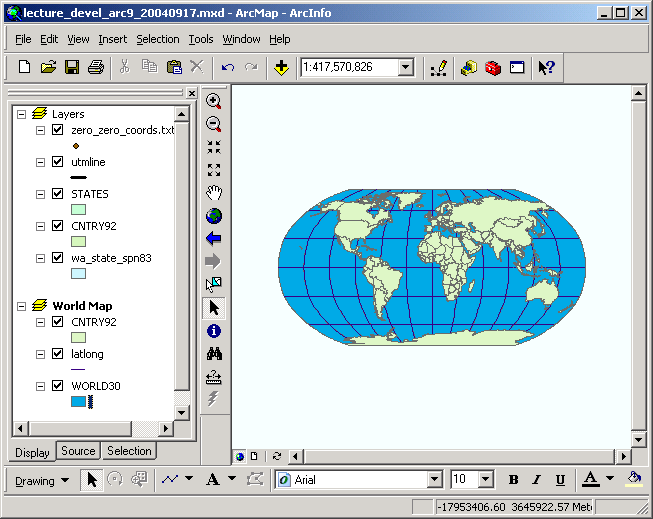 Properties Shape: Shape distortion is very low within 45° of the origin and along the Equator. Area: Distortion is very low within 45° of the origin and along the Equator. Management: Generally distorted. Distance: Generally, scale is made true forth latitudes 38° N and S. Scale is constant forth any given latitude, and for the latitude of opposite sign. |
| Lambert (planar) | 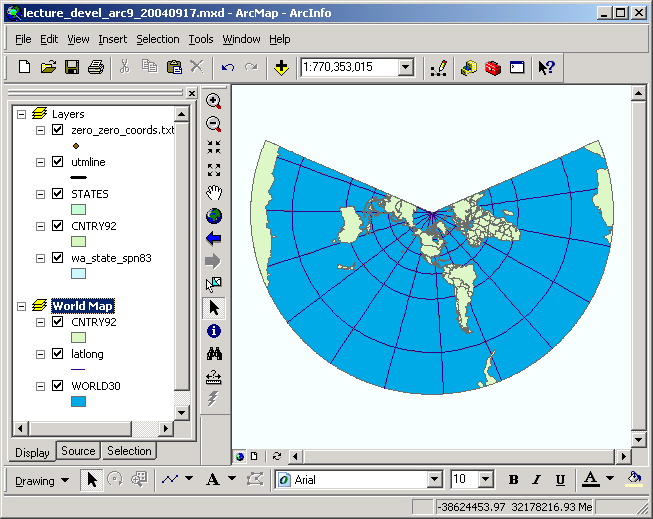 Properties Shape: Shape is minimally distorted, less than 2 pct, within 15° from the focal point. Beyond that, athwart distortion is more pregnant; pocket-size shapes are compressed radially from the eye and elongated perpendicularly. Surface area: Equal-expanse. Direction: Truthful management radiating from the central betoken. Altitude: True at center. Scale decreases with altitude from the center along radii and increases from the middle perpendicular to the radii. |
| Mollweide | 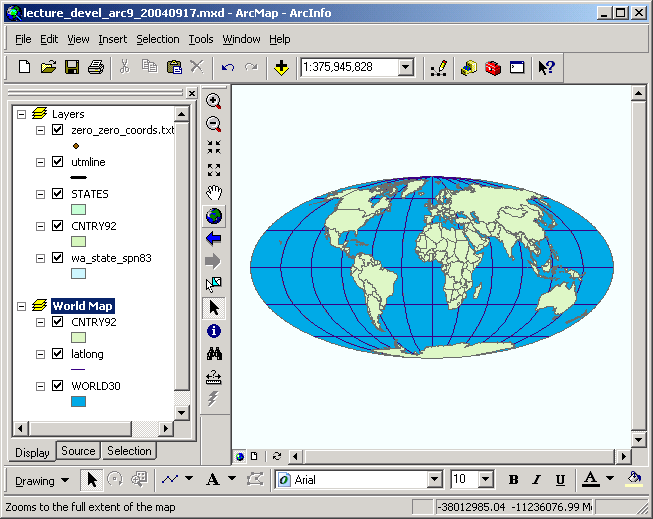 Backdrop Shape: Shape is not distorted at the intersection of the cardinal superlative and latitudes xl° 44' Due north and S. Baloney increases outward from these points and becomes severe at the edges of the projection. Area: Equal-expanse. Direction: Local angles are truthful only at the intersection of the central superlative and latitudes 40° 44' Due north and S. Direction is distorted elsewhere. Distance: Scale is true along latitudes 40°44' N and S. Distortion increases with distance from these lines and becomes severe at the edges of the projection. |
| Orthographic | 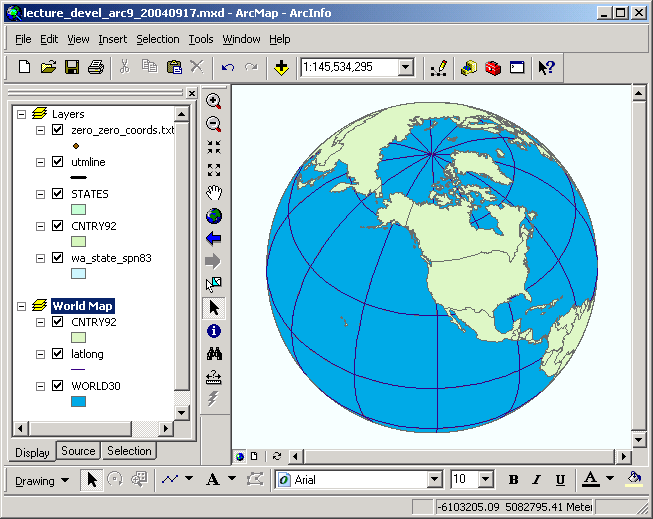 Properties Shape: Minimal distortion nearly the middle; maximal distortion near the border. Area: The areal calibration decreases with distance from the center. Areal calibration is zero at the edge of the hemisphere. Direction: True direction from the central point. Distance: The radial scale decreases with distance from the center and becomes naught on the edges. The scale perpendicular to the radii, forth the parallels of the polar aspect, is accurate. |
| Albers (conic) | 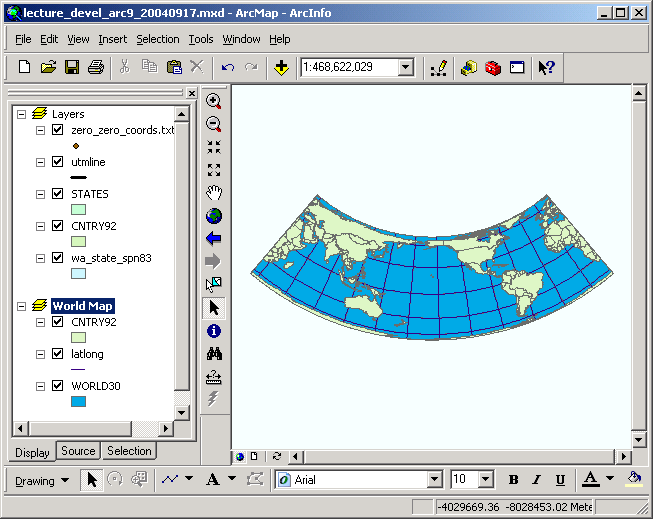 Backdrop Shape: Shape is true forth the standard parallels of the normal aspect (Blazon 1), or the standard lines of the transverse and oblique aspects (Types two and 3). Distortion is severe near the poles of the normal aspect or 90° from the central line in the transverse and oblique aspects. Surface area: There is no area baloney on any of the projections. Direction: Local angles are correct along standard parallels or standard lines. Direction is distorted elsewhere. Distance: Calibration is truthful forth the Equator (Type i), or the standard lines of the transverse and oblique aspects (Types 2 and 3). Scale baloney is severe near the poles of the normal attribute or 90° from the cardinal line in the transverse and oblique aspects. |
For more complete discussions of map projections and related topics, run into these resources, or perform a web search:
- Karen Mulcahy'southward Map Projection Home Folio
- Geodetic Datum Overview, Section of Geography, University of Colorado at Boulder
- Global Positioning System Overview, Department of Geography, University of Colorado at Bedrock
- Coordinate Systems Overview, Department of Geography, University of Colorado at Boulder
- ArcGIS Help
Projecting spatial datasets
ArcGIS at version nine supports projection transformations of both vector and raster data.
You may take information that are stored unprojected (i.e., the data have internal coordinates representing latitude and longitude measurements); other data may be stored in a projection/coordinate system such every bit Land Plane or UTM. In that location are several possible options for projection transformations, based on how your data are stored:
- Unlike datasets stored in different projections.
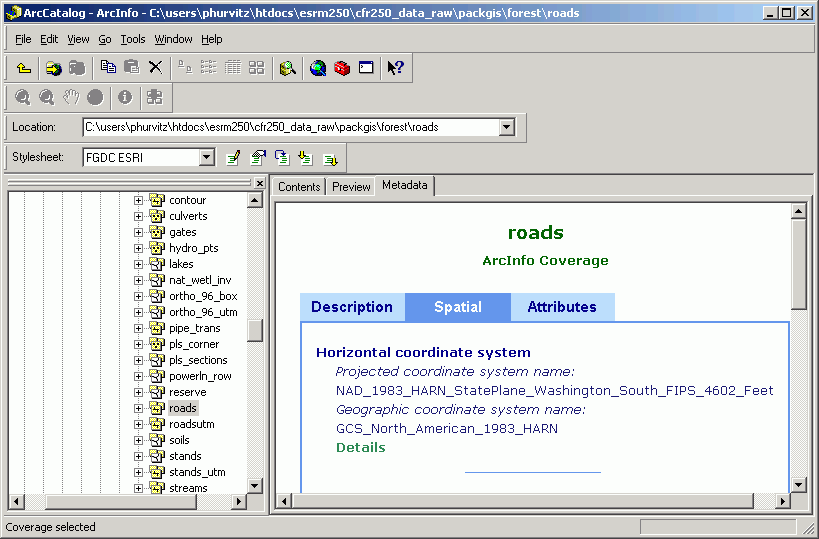
- If projection is defined for each file. You can tell this is the case because each dataset will show its projection in ArcCatalog (Metadata > Spatial). There volition be a description for Horizontal coordinate system. In this case, ArcMap should have no problem displaying these datasets at the same time. If ArcMap can read the project parameters for both datasets, it will project one of them "on the wing" for display purposes.
Here is an ArcInfo coverage stored in Country Airplane:
And a coverage stored in UTM:

Both displayed at the same time:
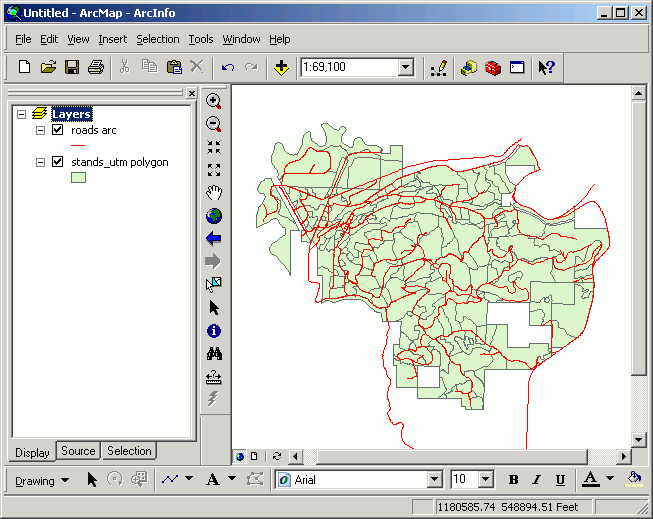
- If projection is undefined for 1 or more of the files. You tin tell this from ArcCatalog as well. If there is no project defined, there will be no description for Horizontal coordinate system. In this case, the datasets will non be able to be displayed simultaneously.
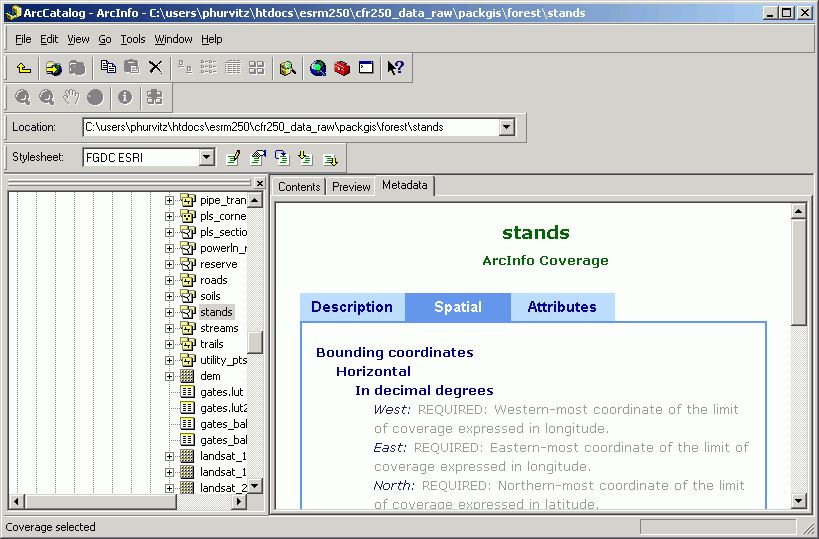

Note that both layers are turned on, but only one displays.
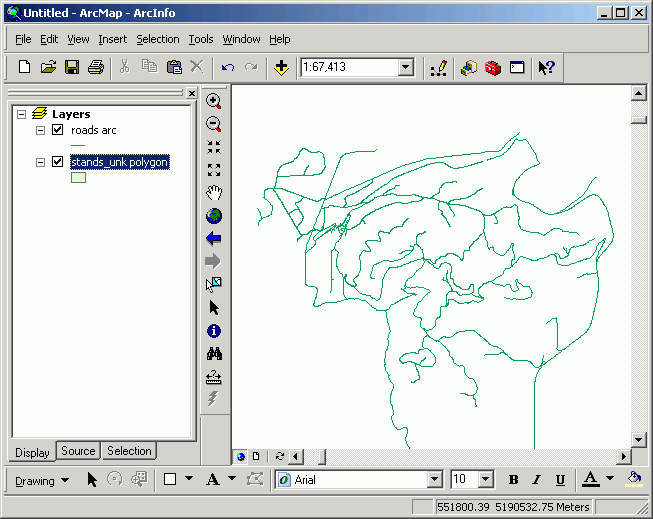
- If projection is defined for each file. You can tell this is the case because each dataset will show its projection in ArcCatalog (Metadata > Spatial). There volition be a description for Horizontal coordinate system. In this case, ArcMap should have no problem displaying these datasets at the same time. If ArcMap can read the project parameters for both datasets, it will project one of them "on the wing" for display purposes.
- Different datasets stored in the same projection.
- If datasets share the same projection, they will display simultaneously if the project is divers.
- If datasets share the same project, they volition display simultaneously even the projection is undefined for i or more of the datasets.
ArcGIS will always attempt to project the view of information on the fly. A data frame's properties can be inverse to match any supported projection/coordinate organization. In this instance, new datasets are not created, but only the view is inverse. Yous can think of this equally putting on different pairs of glasses, each one of which is a different project. When you "view" unprojected or Country Plane data with the UTM "glasses," your data will appear to be projected to UTM. If yous view unprojected or UTM data with the Land Airplane "glasses," your data will announced to be projected to State Plane. However, y'all have not actually changed the data in any way, you have but changed the manner you are looking at the data. When unprojected data are displayed in a view, they are by default shown in a display that appears similar to the Plate Carée projection.
If y'all are only displaying data together, information technology is fine to mix datasets that are stored with different projection parameters. However, if you are doing any analytical work, information technology is e'er suggested to make certain your datasets are stored in the same projection.
Too, information technology is always recommended to make sure your datasets have projections defined. That way, if at that place is any confusion, either for the programmer or some other user, one can always view the projection information.
A number of these situations will exist covered in lab session.
How projections work on a programmatic level
Each different project is a mathematical function that takes coordinate pairs as inputs [(x, y)], and generates new coordinate pairs as output [f(x, y)], every bit shown in the generic part below. The projection function is symbolized by f .
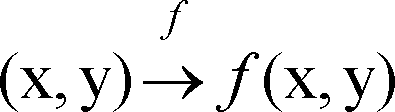
| input | output |
| angles | Cartesian coordinates |
| Land Airplane | UTM |
| Miller Cylindrical | Lambert Azimuthal |
Here is an example of how a projection changes a set of coordinates. The original longitude/latitude coordinate is somewhere within Seattle.
| Projection, zone, datum (units) | Ten | Y |
| geographic, NAD27 (decimal degrees) | -122.35° | 47.62° |
| UTM, Zone 10, NAD27 (meters) | 548843.5049 | 5274052.0957 |
| State Aeroplane, WA-N, NAD83 (anxiety) | 1266092.5471 | 229783.3093 |
Each of the projections in this case (UTM, Country Plane), are governed by a different set up of projection functions, and therefore issue in unlike output values from the same input value.
If you consider the vector data model, every point has a coordinate; every line'due south nodes and vertices have coordinates; and every polygon's outlines have coordinates. Project of a dataset from one system to some other is simply the process of applying the project function to each coordinate in the dataset. The larger and more complex a dataset, the longer information technology volition have to perform the projection.
You should be aware of a fundamental departure betwixt projecting a dataset and simply applying a projection to a data frame. In the onetime case, each pair of input coordinates has a new output coordinate location calculated. In the latter case, some generalization of information is used in social club to speed display. When authentic and precise measurements are needed, e'er project the datasets themselves, rather than just projecting the data frame.
Return to top | Ahead to Help Topics
 | The Academy of Washington Spatial Technology, GIS, and Remote Sensing Folio is supported by the School of Forest Resources | School of Forest Resources |
Source: https://courses.washington.edu/gis250/lessons/projection/


0 Response to "The Main Reason You Need to Know the Projection of Data"
Post a Comment